Definimos la exponencial compleja de un número z D x C i y como:
f(z) = ez z = x + iy
f(z) = ex+iy = ex . eiy
TEOREMA DE EULER
eiy = (cos y + i sen y)
f(z) = ex (cos y + i sen y)
PROPIEDADES
1. ez es analítica
2. ez. ew = ez+w ; ∀ z,w ∈ C
3. ez ≠ 0 ∀ z ∈ C
4. e-z = 1/ez , ∀ z ∈ C
5. ez/ew = ez-w
6. Si x ∈ ℝ -> |eix| = 1
7. ez = 1 <-> z = 2πki ; k ∈ z
8. ez = ew <-> z = w + 2πki

PROPIEDADES
1. elog z = z
2. log z + log w = log(zw) ∀ z,w ∈ C
3. log z – log w = log(z/w) ∀ z,w ∈ C
4. log zα = α log z ; α ∈ C
5. Zw = ew log z
FUNCION TRIGONOMETRICA
INTEGRAL COMPLEJA
Como siempre, luego de definir la derivada, construimos el concepto de integral a partir de la
suma de Riemann. Esto es:
PROPIEDADES
La integración compleja tendrá las propiedades acostumbradas :
CURVAS SUAVES E INTERVALOS
una curva γ en el plano complejo es el conjunto de puntos (x,y) tal que
INTEGRALES DE LINEA
PROPIEDADES
PROPIEDAD 1
Sean I = [a, b], γ: I −→ C un camino regular a trozos, f, g: γ(I) −→ C
continuas. λ, µ ∈ C. Entonces,
a) Para todos λ, µ ∈ C,
PROPIEDAD 2
Sean I = [a, b], A un subconjunto abierto de C y f una funci´on anal´ıtica
en A. Si γ: I −→ C es un camino regular a trozos tal que γ(I) ⊆ A entonces :
.png)
LOGITUD DE UNA CURVA
INTEGRALES CERRADAS
para que se diga que es una integral cerrada, la unica condicion adicional es que la curva suave sea una cuerva cerrada.
PROPIEDADES
INTEGRAL DE CAUCHY
Sea f(z) una funcion holomorfa en un ´
dominio Ω ⊂ C que contiene el contorno cerrado simple orientado positivamente
γ y su interior. Si a es un punto del interior de γ, entonces
Como f es continua en a, para cada ǫ > 0 habra un entorno ´ D(a, δ) tal que
si z ∈ D(a, δ), entonces |f(z) − f(a)| < ǫ. Tomemos ahora un 0 < ρ < δ tal que
la circunferencia
C = {z ∈ C : |z − a| = ρ}
este contenida ıntegramente en el interior de γ. Como f(z)/(z − a) es holomorfa
en γ, C y entre ambos contornos
PROPIEDAD 2
si f es analitica en un dominio simplemente conexo D, entonces la integral es independiente de la trayectoria .
siendo γ1 y γ2 so trayectorias diferentes

PROPIEDAD 3
TEOREMA DE LA DEFORMACION
Sea f una funcion analitica en un dominio D, excepto en z0 y sean curvas cerradas simples que encerran a z0

PROPIEDAD 4
INTEGRAL DE CAUCHY
Si f es analitica en un dominio D simplemente conexo , Sea γ cualquier curva cerrada sim'le en D, que encierre a Zo
INTEGRAL 5
INTEGRAL DE CAUCHY PARA DERIVADAS SUPERIORES
si f es analitica en un dominio D simplemente conexo. Sea γ cualquier curva cerrada simple en D, que encierre a Zo
SERIES Y SUCECIONES
SUCECIONES
SUCECIONES
Una sucesion compleja es una funcion de los numeros naturales sobre los numeros complejos.
f(n) = in
Los elementos de la sucesion:
{i0, i1, i2, i3, . . . in, . . . }
Una sucesion se denota por { Zn }
PROPIEDADES
- Sea Zn = Xn + iYn, para cada entero positivo "n" y sea L = a + ib, entonces:
Limn à ∞ Zn = L ßà Limn à ∞ Xn = a ˄ Limn à ∞ Yn = b
Si { Zn } à L ˄ Si { Wn } à K, entonces:
- { Zn } + { Wn } à L + K
- { α Zn } à α L
- { Zn Wn } à (L)(K)
- { Zn / Wn } à L/K ; Wn ≠ 0 ; k ≠ 0

CRITERIO DE LA RAZON
CRITERIO DE LA RAIZ
SERIES ESPECIALES
SERIES GEOMETRICAS

SERIES DE POTENCIA

SERIES ARMONICAS
CRITERIO DE LA RAIZ
SERIES ESPECIALES
SERIES GEOMETRICAS

SERIES DE POTENCIA

SERIES ARMONICAS

INFORMACION TOMADA DE :












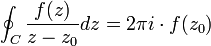




Excelente
ResponderEliminar