Empezamos este curso con gran animo y optimismo, con indicaciones generales y temas establecidos.
Primera Semana
- Todo numero real es un numero complejo
- existen numeros complejos que no son reales
Si y = 0 el número complejo se reduce a un número real ya que x + 0i = x.
Si x = 0 el número complejo se reduce a yi, y se dice que es un número imaginario puro.
El conjunto de todos números complejos se designa por  .
.
 .
.
tenemos:
Cuando no hay parte imaginaria, como en este caso, se dice que el complejo es real.
Entonces los Numeros Reales forman parte del conjunto de los Números Complejos.
Cuando un numero complejo no tiene parte real, como en el presente caso, se dice
que es un imaginario puro.
NUMEROS COMPLEJOS IGUALES
Dos números complejos z1 = a + bi y z2 = c + di son iguales sı y solo si a = c y
b = d. En otras palabras, dos números complejos son iguales cuando sus componentes
respectivas, real e imaginaria, son iguales.
SUMA DE COMPLEJOS
Sean z1 = X1 + Y1i y z2 = X2 + Y2i dos numero ´ s complejos. Entonces la suma de
z1 con z2, denotada por z1 + z2 es el numero ´ complejo
z1 + z2 = (X1 + X2) + (Y1 + Y2)i
Ejemplo. Para sumar z1 = 3 + 2i con z2 = −8 + 4i hacemos
z1 + z2 = (3 + 2i) + (−8 + 4i) = (3 − 8) + (2 + 4)i
z1 + z2 = −5 + 6i
PROPIEDADES
- Z + (W + U) = (Z + W) + U
- Z + U = U + Z
- Z + 0 = (x + yi) + (0 + 0i) = (x + 0) + (y + 0)i = x + yi = Z
- Z + (−Z) = (−Z) + Z = 0
tenemos:
Sean Z = a + bi y W = c + di definimos su producto, mediante la f´ormula
Z · W = (ac − bd) + (ad + bc)i
(a + bi)(c + di) = ac + adi + bic + bdi^2
CONJUGADO
Definición = x+ yi es un numero ´ complejo, entonces el Conjugado de Z, denotado por Z, es otro numero ´ complejo definido por
Ejemplo. Si Z = 2 + 9i, su conjugado es Z = 2 − 9i
DIVISION
Si Z y W son dos numero ´ s complejos, y W 6= 0, podemos hacer la division de Zentre W de la forma siguiente
Z
Z
W
=
Z
W
·
W
W
=
Z · W
|W|
2
Si hacemos Z = x+yi y W = c + di, tendremos Z W = (ac + bd) + (bc − ad)i a^+b 2
Si hacemos Z = x+yi y W = c + di, tendremos Z W = (ac + bd) + (bc − ad)i a^+b 2
FORMA POLAR
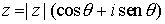
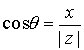 ,
, 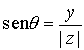 .
.
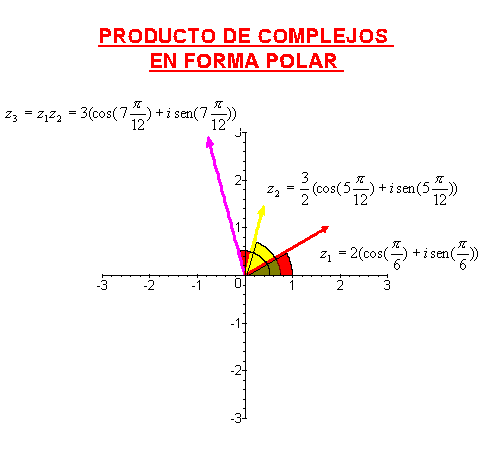
Otra forma de expresar un número complejo es la forma polar o forma módulo-argumento,
donde 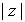 es el módulo de
es el módulo de  , y donde q es un argumento de
, y donde q es un argumento de  , esto es, q es un ángulo tal que
, esto es, q es un ángulo tal que
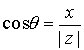 ,
, 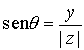 .
.
FORMA EXPONENCIAL
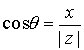 ,
, 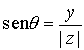 .
.

LIMITES DE UNA FUNCION DE VARIABLE COMPLEJA
Para cada n´umero real ε > 0 existe un n´umero real δ > 0 tal que si 0 < |z − z0| < δ , entonces |f(z) − l| < ε.
f ∈ C/a := ∀ ǫ > 0 , ∃ δ > 0 : ∀ z ∈ {z : |z − a| < δ} ∩ D =⇒ |f(z) − f(a)| < ǫ

CONTINUIDAD
La función f(z) es continua en el punto z0 si se cumple que
limz→z0 f(z) = l,
EJEMPLO:
ANALIZAR SU CONTINUIDAD
DERIVADAS DE LAS FUNCIONES DE VARIABLES COMPLEJAS




donde 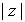 es el módulo de
es el módulo de  , y donde q es un argumento de
, y donde q es un argumento de  , esto es, q es un ángulo tal que
, esto es, q es un ángulo tal que
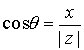 ,
, 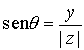 .
.
POTENCIAS Y RAICES
Todo numero complejo tiene exactamente n raíces n-esimas.
Ası por ejemplo 1 tiene 4 raíces cuartas, pues:
1
4 = i
4 = (−i)
4 = (−1)
4 = 1
FUNCIONES DE VARIABLE COMPLEJA
Sea S un conjunto de números complejos. Una función f de variable compleja definida en S es
una regla que asigna a cada número complejo z = x + iy de S, algún número complejo w = u + iv.
El número complejo w se llama valor de f en z y se denota por f(z), es decir
w = f(z), (2.1)
y el conjunto S donde está definida la función f(z) se llama dominio de f.
Dado que z y w son números complejos, relacionados por la función f, es posible escribir
w = f(z)
u + iv = f(x + iy)
donde hemos considerado que
w = u + iv
y
z = x + iy.
Lo anterior permite expresar a la función de variable compleja f(z) como la suma
f(z) = f(x, y) = u(x, y) + iv(x, y)
f(z) = Re(f(z)) + i Im(f(z)) = u(z) + iv(z)
Como C = IR2
, una función compleja lleva asociada una función f: A ⊆ IR2 −→ IR2 donde
f(x, y) = f(x + iy) y que tiene por componentes, f = (u, v), las funciones u(x, y) = u(x + iy)
y v(x, y) = v(x + iy). As´ı pues, toda función compleja de variable compleja equivale a un par
de funciones reales de dos variables reales
REPRESENTACIONES GRAFICAS
- El dominio de f(z) es todo el plano complejo o una region
- El recorrido o rango de f(z) es una parte o todo el plano complejo
- Se evidencia la necesidad de graficar f(z) en R^n, pero esta no es posible

Para cada n´umero real ε > 0 existe un n´umero real δ > 0 tal que si 0 < |z − z0| < δ , entonces |f(z) − l| < ε.
f ∈ C/a := ∀ ǫ > 0 , ∃ δ > 0 : ∀ z ∈ {z : |z − a| < δ} ∩ D =⇒ |f(z) − f(a)| < ǫ

CONTINUIDAD
La función f(z) es continua en el punto z0 si se cumple que
limz→z0 f(z) = l,
EJEMPLO:
ANALIZAR SU CONTINUIDAD
DERIVADAS DE LAS FUNCIONES DE VARIABLES COMPLEJAS
FUNCIONES ANALITICAS
ECUACION DE CAUCHY RIEMAN




INFORMACION TOMADA DE:
http://wmatem.eis.uva.es/~matpag/CONTENIDOS/Complejos/marco_complejos.htm
http://rpduarte.fisica.uson.mx/archivos/curso3/02-MetMatFisI.pdf
http://rpduarte.fisica.uson.mx/archivos/curso3/02-MetMatFisI.pdf







No hay comentarios:
Publicar un comentario